Éste es el tercer capítulo de la serie, aquí tienes los enlaces de los dos artículos previos:
En capítulos anteriores …
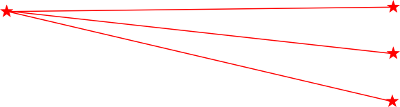
Partiendo de una escena ficticia, comenzamos nuestra experiencia con el primer viajero, el fotón. En el primer post vimos cómo se desplazaba el fotón desde su origen (en el ejemplo, el sol) hasta el objeto visible, y cómo se reflejaba en éste y se dirigía a nuestros ojos. Al final del post planteamos el problema de la organización: todos los objetos a la vista mandaban innumerables fotones en todas direcciones. Un sólo objeto envía sus fotones reflejados en dirección divergente:
En cuanto añadimos un segundo objeto, proyecta sus fotones de forma difusa, de forma que coinciden en el espacio los fotones de ambos objetos:
Así no podríamos obtener información visual: necesitamos ordenarla, separarla. De este reto trataba el siguiente post. En esta segunda parte descubrimos que la «magia» ocurría gracias a un fenómeno físico llamado refracción, que implicaba un cambio de dirección del rayo de luz al pasar de un medio transparente a otro. En concreto, la peculiar forma de la córnea (es convexa como si formara parte de una esfera) hacía que los rayos divergentes de un objeto se volvieran convergentes.
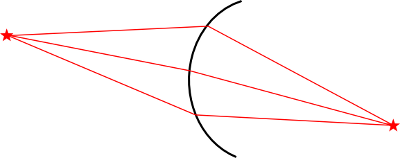
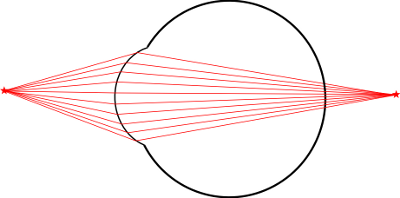
El efecto con un sólo punto emisor de fotones sería este:
Los rayos que llegan divergentes, después de pasar por la córnea, se hacen convergentes y confluyen en una posición concreta por detrás de ésta.
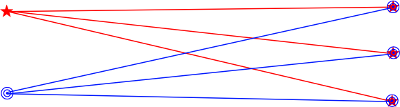
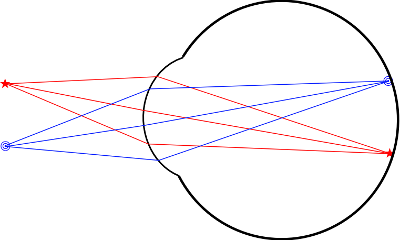
Si ponemos dos puntos emisores, lo que ocurre es esto:
Los rayos de cada punto confluyen por separado en lugares diferentes. Ya tenemos la información ordenada. Los puntos que vienen de la parte superior van abajo, los que llegan desde la parte inferior se proyectan arriba. De igual manera la luz de la izquierda va a la derecha, y viceversa. Se forma una imagen invertida por detrás de la córnea. Así pudimos establecer el primer modelo teórico, en el que la córnea era capaz de hacer converger perfectamente todos los rayos que llegaban del exterior.
Si efectivamente la córnea fuera una lente que se ajustara al modelo teórico ya tendríamos solucionado el problema óptico: obtendríamos una imagen proyectada en el fondo del ojo. La cosa quedaría más o menos así:
La córnea queda insertada en la parte delantera de lo que sería el «armazón» del ojo. Los puntos del exterior se proyectan de forma nítida en la parte posterior del ojo.
Problemas
Fácil, ¿no?. Bueno, por desgracia (realmente, por suerte), nuestro ojo no se ajusta realmente a esta situación perfecta. Hay tres problemas fundamentales.
Primer problema: nos faltan dioptrías
Nos toca echar un vistazo a unos números. [No voy a poner los cálculos, que si bien son sencillos complicarían innecesariamente la explicación. En cualquier libro de óptica humana aparecen. Y si alguien tiene alguna duda, no tengo ningún problema en desarrollarlos en los comentarios].
La potencia de una lente depende de su curvatura: cuanto más curva es su superficie, más desvía los rayos luminosos. Así, una lente convexa con la curvatura muy pronunciada converge mucho los rayos que llegan, y el punto donde los rayos se cruzan está cerca de la lente. Por el contrario, si la lente es menos curva tiene menos potencia el punto se va más lejos.
El radio de curvatura de la cara anterior de una córnea de potencia media es de unos 7.8 mm, lo que produce una potencia de 48 dioptrías, aproximadamente. Sin embargo, la cara posterior de la córnea también tiene su acción refractiva, y hay que tenerlo en cuenta. Cuando el rayo luminoso pasa de la córnea al humor acuoso (el fluido que rellena el interior de la parte delantera del ojo, formado básicamente de agua) se refracta, pero los rayos no se hacen más convergentes, sino al contrario: divergen. El radio de curvatura de la cara posterior es de 6.5mm, lo que nos da una potencia de -6 dioptrías aproximadamente. Toma el signo negativo porque hace diverger los rayos, en vez de convergerlos. Por lo tanto, la potencia total de la córnea es de unas 42 dioptrías.
Una lente de 42 dioptrías es capaz de converger los rayos que vienen de un foco luminoso lejano en un punto situado a unos 32 mm por detrás. Pero el caso es que el ojo, desde la córnea hasta su parte posterior mide bastante menos, en general, unos 23 mm.
La proyección quedaría así:
La imagen se nos va hacia atrás. Nos falta más potencia. Para un tamaño habitual de ojo, requerimos aproximadamente 60 dioptrías, y la cornea por sí sola no nos ofrece toda esta graduación.
Segundo problema: los rayos periféricos convergen antes
Vamos a suponer por un momento que la córnea tiene efectivamente 60 dioptrías y el primer problema estaría solucionado. Las lentes esféricas, como la que hemos asumido en el modelo teórico, funcionan bien enfocando los rayos divergentes haciéndolos convergentes, pero sólo cuando estos rayos llegan a la parte central de la lente. La parte periférica de la lente tiene más potencia que la parte central, por lo que los rayos convergen antes.
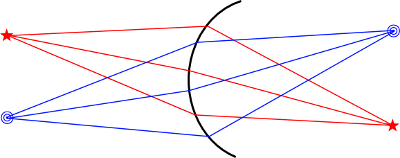
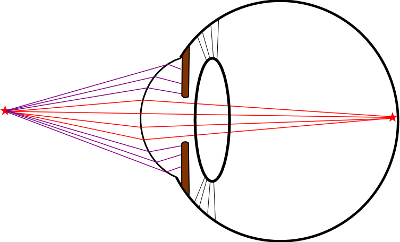
Lo vemos más fácil en un dibujo:
Los rayos que atraviesan la córnea por su parte central están dibujados en rojo, y convergen adecuadamente en la parte posterior del ojo. Sin embargo, la luz que pasa por la zona periférica de la córnea, que he señalado en púrpura, convergen antes. No confluyen en la parte posterior del ojo, sino que se entrecruzan por delante. Este problema se llama aberración esférica.
Tercer problema: la distancia cuenta
Hasta ahora hemos estado considerando que había un solo punto luminoso, o bien dos puntos que están a la misma distancia del ojo. Y aunque no estaba mencionado antes, el cálculo de las 60 dioptrías necesarias se refiere a un objeto lejano, unos 6 metros o más. Sin embargo, ¿qué pasa si estamos mirando un objeto cercano?. Los rayos llegan más divergentes, así que lo de las 60 dioptrías ya no nos sirve.
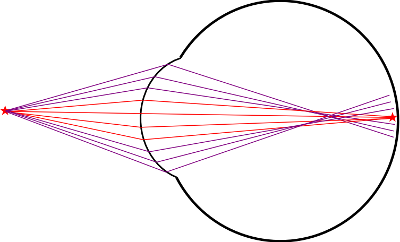
Veámoslo en una imagen. Suponiendo que el ojo tuviera una potencia óptica de 60 dioptrías, el objeto lejano (en rojo) queda enfocado perfectamente en la retina. Sin embargo, el objeto cercano (azul) queda por detrás.
Si quisiéramos enfocar el objeto azul necesitamos más potencia de lentes que para enfocar el objeto rojo. Y cuando más cerca está el objeto más divergentes nos llegan sus rayos de luz, por lo que más dioptrías necesitaremos.
Herramientas
Ya hemos planteado los tres problemas que tenemos que solucionar. Ahora tenemos que conocer qué elementos tiene el ojo para solucionarlos y permitir que el viaje de nuestro fotón por el interior del globo ocular llegue a buen puerto.
Primera herramienta: la forma real de la córnea
Para hacer cálculos y para tener un modelo teórico fácil de entender, hemos asumido que la córnea tiene forma esférica. Y es cierto para la zona central, así que los cálculos cuadran. Sin embargo, por fuera de los 3-4 milímetros centrales, la cosa cambia. La curvatura disminuye conforme vamos a la zona periférica. Dicho de otro modo, la curvatura de la córnea no es igual en toda la superficie. En la zona central es más curva, y en la parte periférica menos (1).
En el dibujo siguiente vemos una esquema en dos dimensiones de una superficie esférica, con una curvatura igual en todos sus puntos. Debajo está representada la córnea, que tiene una curva más acentuada en el centro y es más plana en la periferia:
Ahora veamos cómo se comporta ópticamente cada superficie. En la siguiente imagen vemos qué ocurre con la superficie esférica: los rayos que la atraviesan por la periferia se encuentran más desviados. Se trataría de una aberración esférica importante.
Sin embargo, en la córnea los rayos periféricos sufren menos convergencias y convergen muy próximos a los rayos centrales. La aberración esférica es mucho menor. Todavía los rayos no están totalmente enfocados, pero la situación es claramente mejor que si tuviéramos un perfil corneal esférico.
Cuando hablamos de medidas de curvatura y potencia corneal (lo que se denomina queratometría) nos referimos realmente a los 3 milímetros centrales de la córnea. Veremos que aunque la potencia de la córnea varía del centro a la periferia, la que define los cálculos que realizamos es la zona central.
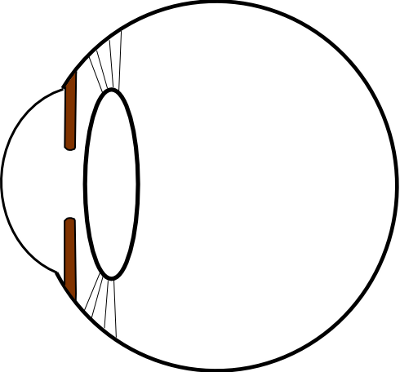
Segunda herramienta: el iris
El iris es un diafragma que modula la entrada de luz en el ojo. Concretamente deja pasar los rayos que pasan por el centro de la córnea y pero no los que cruzan la periferia. Con lo cual, es una solución bastante eficaz para la aberración esférica que comentábamos hace un momento. Vemos en este dibujo que los rayos púrpura que entran por la zona exterior son bloqueados.
[En seguida vamos a ver que es un sistema redundante: la aberración esférica se soluciona con el cristalino, de forma que un individuo joven y sano no precisa del iris y la pupila para corregir esta aberración.]
No sólo es una solución muy válida para esta aberración esférica, sino para otras que he preferido no mencionar que las podemos agrupar como aberraciones periféricas (coma, astigmatismo oblicuo, etc). Se originan en la parte periférica de la córnea. Si bien la zona central es muy regular y con una curvatura esférica casi perfecta, en la periferia no ocurre eso. Esta zona exterior en general es más plana y no produce tanta aberración esférica como explicábamos más arriba, pero no tiene una curvatura perfecta, existen irregularidades. El iris impide que los rayos desviados por la periferia lleguen más atrás. Por lo tanto, los rayos que pasan por la pupila están bastante libres de aberraciones en general (2).
Tercera herramienta: el cristalino
Todavía nos queda el problema más importante: de las 60 dioptrías que necesitamos, la córnea sólo nos aporta 42. Y la solución la tenemos en forma de una lente adicional: el cristalino. El cristalino es una lente que poseemos dentro del ojo, por detrás del iris. Tiene forma de lenteja y se encuentra sujeto por numerosos y pequeños ligamentos. Ópticamente el cristalino es un sistema complicado, porque tiene diferentes interfases en su interior. Si bien es menos potente que la córnea en dioptrías, es mucho más complejo. No vamos a entrar en detalles y simplificaremos al máximo, asumiendo que es una única lente convergente no esférica.
Entonces, ¿qué nos aporta el cristalino?
- Las dioptrías que nos faltan: Se trata de una lente positiva o convegente, al igual que la córnea, con una potencia media en torno a las 18 dioptrías. Si sumamos este valor con las 42 dioptrías de potencia convergente de la córnea obtenemos las 60 dioptrías que necesitamos. De esta manera, por fin hemos conseguido que un objeto lejano se enfoque adecuadamene en la parte posterior del ojo.
- Su potencia es variable: Las 18 dioptrías que acabamos de mencionar se obtienen en la situación, digamos, «normal». El cristalino, a diferencia de la córnea que tiene una potencia fija, es capaz de modificar su forma aumentando sus dioptrías. La situación por defecto es que los ligamentos están tirantes y la tensión hacia la parte periférica y la forma de lenteja del cristalino induce una potencia de 18 dioptrías. Esta tensión es pasiva, producida por la situación y proporción de las estructuras. En la zona de anclaje de los ligamentos del cristalino hay un músculo, el músculo ciliar. Cuando se contrae, la tensión de los ligamentos se relaja. El cristalino, al verse sometido a una relajación de las fuerzas que lo estiran, cambia su forma. Adquiera una morfología más esférica, aumentado su curvatura tanto anterior como posterior. De esa forma, aumenta su potencia en dioptrías. En situaciones normales el cristalino no suele modificarse hasta más allá de las 24 dioptrías, aunque un niño puede llegar a las 35 dioptrías. Este fenómeno se llama acomodación, y sólo va en un sentido: podemos aumentar la potencia en dioptrías, pero no disminuir. Es decir, si el cristalino en reposo tiene 18 dioptrías, podremos conseguir 20 ó 22 si las necesitamos, pero no podemos conseguir 16. Cuando nacemos tenemos una capacidad máxima de acomodación: podemos añadir unas 15 dioptrías a lo que tuviera el cristalino relajado. Con el crecimiento vamos perdiendo acomodación, de forma que con 35 años nos quedan 7 dioptrías de acomodación y con 45 años tenemos 4 dioptrías. Bien, ¿y para qué queremos la acomodación?. Principalmente para solucionar el tercer problema que hemos comentado antes, lo que titulábamos «la distancia cuenta». Para enfocar un objeto cercano necesitamos incrementar la potencia del sistema óptico, y eso nos ofrece la acomodación. En otro artículo de la serie veremos que también es útil para alguna otra cosa.
- Tampoco es esférico. En conjunto, el cristalino no se comporta como una lente esférica. Decíamos antes, al hablar de la córnea, que una lente esférica hace que los rayos periféricos converjan antes que los centrales. La córnea no se comportaba así: era más plana en la periferia y más curva en el centro para evitar en parte este problema. Pero no lo evita del todo. El cristalino hace el resto: los rayos que vienen de la periferia modifican menos su trayectoria que los rayos centrales. De forma que entre la córnea y el cristalino la aberración esférica queda solucionada. Por lo menos en un ojo joven y sano.
Soluciones
Al ir describiendo las herramientas que tiene el ojo para «afinar el enfoque» ya hemos ido proponiendo las soluciones, pero vamos a repasarlas
El enfoque a todas las distancias
Sumando los efectos ópticos de córnea y cristalino (en reposo) ya obtenemos la potencia para enfocar un objeto lejano (en el ejemplo: 42 + 18 = 60). Cuando miramos un objeto cercano los rayos llegan más divergentes, por lo que necesitamos más potencia. Para un objeto a 33 centímetros del ojo necesitaríamos 3 dioptrías más. El cristalino cambia su curvatura mediante un proceso activo llamado acomodación. Por otra parte, el iris es capaz de ofrecernos una ayuda adicional cuando la pupila se cierra, atenuando el desenfoque cuando la adaptación del cristalino a la distancia cercana no es exacta.
La aberración esférica
El desenfoque de los rayos periféricos se soluciona gracias a que las lentes del ojo no son esféricas, sino más curvas en el centro que en la periferia. Así, tanto la córnea como el cristalino colaboran en solucionar el problema.
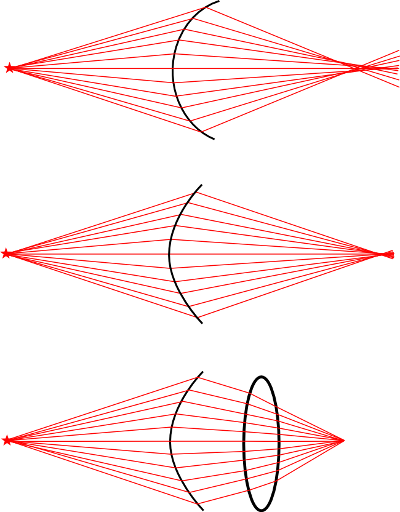
En el dibujo de abajo vemos cómo se comporta una lente esférica (mucha aberración esférica), la córnea (poca aberración esférica), y la córnea junto con el cristalino (sin aberración esférica)
Si bien en un ojo sano y joven no se requiere una medida adicional, cuando envejecemos las cosas cambian. Normalmente es el cristalino que pierde su perfil óptimo con los años. También podemos tener problemas en casos de una óptica ocular «de mala calidad», o cuando el ojo se ha sometido a una cirugía de córnea o cristalino. En estos casos, nuestro salvavidas es el iris: aunque el sistema de lentes induzca una aberración esférica grande, una pupila de menos de 4 milímetros lo soluciona casi por completo, ya que los rayos de la periferia, los que van mal orientados, quedan bloqueados por el iris y sólo pasan al interior los que atraviesan la pupila, que son los centrales y bien enfocados.
—–
1. La córnea normal es prolata, más curva en el centro que la periferia. La situación contraria, una superficie más plana en el centro y más curva en la periferia recibe el nombre de oblata. Estas formas están definidas mediante el coeficiente Q, que mide la asfericidad corneal. Un valor de 0 sería una superficie esférica. Un valor positivo corresponde a una curva oblata, muy infrecuente en córneas sanas no intervenidas. Un valor negativo corresponde a una córnea prolata. Los valores medios de Q es de -0.26. Para eliminar por completo la aberración esférica necesitamos un Q de -0.52. Algunas enfermedades corneales, y sobre todo la cirugía refractiva en la córnea, pueden producir que la superficie corneal pase de prolata a oblata (Q positivo). En consecuencia aparece una aberración esférica muy intensa que puede producir síntomas.
2. El iris también aumenta la profundidad de campo por lo que ayuda también en el problema de enfocar a diferentes distancias. Eso lo conocen bien los que padecen de vista cansada, porque con una luz intensa enfocan mejor de cerca, precisamente porque con más luz el iris se cierra más. Pero prefiero no explicarlo en esta ocasión y centrarme en aspectos más relevantes.











29 octubre, 2012
Una pregunta: Esto es para enfocar bien sobre una superficie curva -la retina- .¿qué diferencia hay para el caso de una cámara donde tenemos una superficie plana? -el sensor-.
Muy bueno el blog.
31 octubre, 2012
Las diferencias son enormes, y muy difíciles de resumir en un comentario. Hay que tener en cuenta un factor principal: en una cámara buscamos la máxima resolución en todos los puntos de la imagen. El ojo precisa la máxima resolución en la zona central del campo visual, pero no lo necesita en la periferia. Existe una pérdida de enfoque conforme nos alejamos del centro de la retina, no debido a su superficie curva, sino al sistema óptico humano en general. Lo que no supone un problema ya que no altera la función de la visión periférica.
6 noviembre, 2012
Muchas gracias, soy abogado pero mantengo desde niño un vivo interés por la ciencia y el c onocimiento en general…ahora ya pensionado y superados los afanes económicos del pasado, he disfrutado con placidez en mi rostro, solo frente al computador, al lograr comprender conceptualmente temas tan complejos, como los tratados en estos tres capítulos…, Estoy realmente impresionado por la sencillez con la que transmiten temas tan complejos, lo cual por mi experiencia me permite concluir que los entienden muy bien.
Mis sinceras felicitaciones
8 noviembre, 2012
Gracias a ti por leerme.
13 noviembre, 2012
Si hay perdida de enfoque al alejarnos de la fóvea por motivos ópticos, ¿será que la disposición de los fotoreceptores y su conexionado responde a esta pérdida? ó hay sólo motivos de ahorrar axones en el nervio óptico? digo, porque en la fóvea hay un nervio por cada fotoreceptor.
gracias por la respuesta.
19 noviembre, 2012
En la retina alejada de la fóvea la imagen llega peor enfocada, con más aberraciones ópticas. Y hay relación entre la menor densidad de fotorreceptores y células ganglionares de esta zona y la menor calidad óptica. No debe entenderse que se ha ido perdiendo «riqueza retiniana» en esa zona. Más bien al revés. Partiendo evolutivamente de ojos más simples, la superioridad óptica y funcional de la fóvea ha permitido un incremento de complejidad estructural ya que, a pesar de suponer una pérdida de recursos, trae consigo un beneficio sensorial que supera con creces los inconvenientes. Una mayor complejidad en la retina periférica no es aprovechado funcionalmente, por lo que evolutivamente no se impone a una periferia más simple.
18 noviembre, 2012
Es este el final del viaje?
Me encantaría seguir con el fotón enfocado en la retina hasta la formación de la imagen.
Sé que este campo está desarrollado por la psicología, pero me encantaría leer una revisión coherente con el nivel de rigor y comprensibilidad del resto del viaje que hemos hecho.
Felicidades por el blog. He aprendido mucho con tus textos.
19 noviembre, 2012
No, todavía no es el final del viaje. De hecho sólo hemos hablado del primer viajero, el fotón. Cuando el fotón estimule al fotorreceptor cambiaremos de protagonista, pero todavía estaremos en el terreno de la oftalmología. Luego entraremos en el terreno de la neuro-oftalmología y neurofisiología visual.
Gracias por leerme.
4 diciembre, 2012
[…] Un viaje por nuestro sistema visual (III) […]
16 marzo, 2013
me pregunta es la siguiente? por que la cornea teniendo una geometria negativa se comporta opticamente como positiva?
17 marzo, 2013
¿Geometría negativa?. La córnea en global es una lente convergente, positiva.
20 marzo, 2014
Buenos días. Soy optometrista en una clínica oftalmológica y estoy realizando un estudio sobre tratamientos personalizados asféricos en cirugía láser excimer. Ahora que estoy «estudiando» sobre aberraciones esféricas, me surgen muchas dudas debido a que cada uno cuenta las cosas de manera completamente diferente. Está claro que la cornea tiene un coeficiente de asfericidad (Q) negativo pero, esto provoca una aberración esférica positiva o negativa? Lo normal es que los rayos marginales se refracten menos por tener menor poder dióptrico en la periferia no? por lo que los rayos marginales inciden por detrás de los axiales, no? y esa AE es positiva o negativa? Estoy muy liada, a ver si me aclarais estas dudas. Gracias.
26 abril, 2014
Hola Leticia:
Una superficie esférica tendría una aberración esférica positiva: los rayos que inciden por la parte periférica se refractan más que los rayos centrales, por lo tanto su punto focal se encuentra por delante. Eso es la aberración esférica positiva.
La córnea normal es prolata, por lo tanto tiene un coeficiente Q negativo. La potencia en la periferia va disminuyendo, en comparación con una superficie esférica. Por lo tanto, los rayos periféricos no se enfocan tan por delante de los rayos centrales. Una córnea prolata, en función del valor de su coeficiente Q, puede tener aberración esférica positiva (menos que en una superficie esférica), aberración esférica cero, o aberración esférica negativa. Todo depende del valor de Q. La mayoría de personas tienen unas córneas con coeficientes Q que compensan en parte la aberración esférica positiva, pero no del todo. Necesitarían ser más prolatas, tener un Q más negativo, para compensar por completo la aberración esférica positiva. Si nos pasamos y el coeficiente Q es más negativo todavía (córneas más prolatas todavía), entonces los rayos periféricos tendrán el punto focal por detrás de los centrales, y entonces tendríamos una aberración esférica negativa.
A ver si esta tabla de sirve de utilidad.
Córnea Oblata (p.ej. tras LASIK) Q>0 Aberración esférica positiva muy alta
Esfera Q=0 Aberración esférica positiva alta
Córnea normal (prolata) Q=-0,26 Aberración esférica positiva baja
Córnea «perfecta» (más prolata) Q=-0,52 Sin aberración esférica
Córnea muy prolata Q < -0,52 Aberración esférica negativa Un saludo.
23 agosto, 2015
[…] A lo largo de cientos de artículos, y usando la divulgación científico-médica he intentado transmitir a mis lectores parte de esa “poesía”, parte de esa belleza que me hace disfrutar de mi trabajo. Pero el blog también ha tenido una función más práctica, el acercar los conocimientos básicos del funcionamiento y las enfermedades del sistema visual al público general. Explicar cómo funciona el ojo normal y cuales son las principales anomalías ha sido ilusionante, y también todo un reto. Por ejemplo, no pensé que me atrevería a hablar de asfericidad corneal, aberración esférica, coeficiente Q, y aspirar a que me entendiera un internauta sin conocimientos específicos previos. Y me atreví. […]
23 mayo, 2017
[…] http://ocularis.es/un-viaje-por-nuestro-sistema-visual-iii/ […]
23 mayo, 2017
[…] Un viaje por nuestro sistema visual (II): Este es el artículo más importante, donde se explica en profundidad cómo los rayos divergentes se proyectan dentro del ojo creando una imagen. Si la explicación no te ha quedado clara, con los esquemas que hay en este artículo probablemente te resulte más sencillo […]
8 septiembre, 2019
[…] esto último es el diseño no esférico de las lentes actuales. Sobre la asfericidad ya hablé en un artículo del blog, en aquella ocasión de la asfericidad del sistema óptico del ojo (córnea y cristalino). Para el […]